mixpp: bdm::ARX Class Reference
bdm::ARX

bdm::ARX Class Reference

Linear Autoregressive model with Gaussian noise. More...

#include <arx.h>

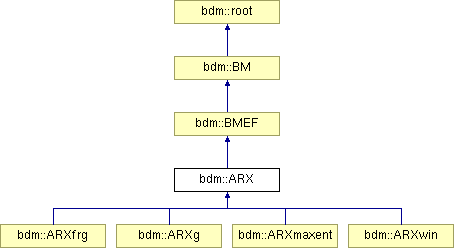
Inheritance diagram for bdm::ARX:

bdm::BMEF bdm::BM bdm::root bdm::ARXfrg bdm::ARXg bdm::ARXmaxent bdm::ARXwin List of all members.

Public Member Functions

void set_statistics (const BMEF *BM0)
 Set sufficient statistics.
void from_setting (const Setting &set)
void validate ()
void set_prior (const epdf *prior)
 function sets prior and alternative density
void set_prior_default (egiw &prior)
 build default prior and alternative when all values are set
void to_setting (Setting &set) const
RV & _rgr ()
 access function
bool _have_constant ()
int _rgrlen ()
Constructors
 ARX (const double frg0=1.0)
 ARX (const ARX &A0)
ARX * _copy () const
void set_frg (double frg0)
void set_constant (bool const0)
void set_statistics (int dimy0, const ldmat V0, double nu0=-1.0)
Mathematical operations
void bayes_weighted (const vec &yt, const vec &cond=empty_vec, const double w=1.0)
 Weighted Bayes $ dt = [y_t psi_t] $.
void bayes (const vec &yt, const vec &cond=empty_vec)
double logpred (const vec &yt, const vec &cond) const
vec samplepred (const vec &cond)
void flatten (const BMEF *B, double weight)
enorm< ldmat > * epredictor (const vec &rgr) const
 Conditioned version of the predictor.
estudent< ldmat > * epredictor_student (const vec &rgr) const
template<class sq_T>
shared_ptr< mlnorm< sq_T > > ml_predictor () const
 conditional version of the predictor
template<class sq_T>
void ml_predictor_update (mlnorm< sq_T > &pred) const
 fast version of predicto
mlstudent * predictor () const
ivec structure_est (const egiw &Eg0)
 Brute force structure estimation.
ivec structure_est_LT (const egiw &Eg0)
 Smarter structure estimation by Ludvik Tesar.
void reduce_structure (ivec &inds_in_V)
 reduce structure to the given ivec of matrix V
Access attributes
return correctly typed posterior (covariant return)

const egiw & posterior () const

Protected Attributes

bool have_constant
 switch if constant is modelled or not
vec dyad
 vector of dyadic update
RV rgr
 RV of regressor.
int rgrlen
 length of the regressor (without optional constant)
egiw est
 posterior density
egiw alter_est
 Alternative estimate of parameters, used in stabilized forgetting, see [Kulhavy].

Detailed Description

Linear Autoregressive model with Gaussian noise.

Regression of the following kind:

\[ y_t = heta_1 \psi_1 + heta_2 + \psi_2 +\ldots + heta_n \psi_n + r e_t \]

where unknown parameters rv are $[ heta r]$, regression vector 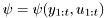$\psi=\psi(y_{1:t},u_{1:t})$ is a known function of past outputs and exogeneous variables 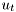$u_t$. Distrubances 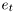$e_t$ are supposed to be normally distributed:

\[ e_t \sim \mathcal{N}(0,1). \]

See Theory of ARX model estimation for mathematical treatment.

The easiest way how to use the class is: 

#include "estim/arx.h"
#include <vector>
#include <iostream>
#include <fstream>
using namespace bdm;
// estimation of AR(0) model
int main(){
        //data
        vector<vector<vector<string>>> string_lists;
        string_lists.push_back(vector<vector<string>>());
        string_lists.push_back(vector<vector<string>>());
        string_lists.push_back(vector<vector<string>>());
        char* file_strings[3] = {"c:\\ar_normal.txt", "c:\\ar_student.txt", "c:\\ar_cauchy.txt"};
        for(int i = 0;i<3;i++)
        {
                ifstream myfile(file_strings[i]);
                if (myfile.is_open())
                {
                        while ( myfile.good() )
                        {
                                string line;
                                getline(myfile,line);
                                vector<string> parsed_line;
                                while(line.find(',') != string::npos)
                                {
                                        int loc = line.find(',');
                                        parsed_line.push_back(line.substr(0,loc));
                                        line.erase(0,loc+1);
                                }
                                string_lists[i].push_back(parsed_line);
                        }
                        myfile.close();
                }
        }
    //prior
    mat V0 = 0.0001 * eye ( 3 );
    //V0 ( 0, 0 ) = 0.1; //
        for(int j = 0;j<string_lists.size();j++)
        {
                for(int i = 0;i<string_lists[j].size();i++)
                {
                        ARX Ar;
                        Ar.set_statistics ( 1, V0 ); //nu is default (set to have finite moments)
                        Ar.set_constant ( false );
                        Ar.validate();
                        // forgetting is default: 1.0
                        vector<vec> conditions;
                        for(int k = 1;k<string_lists[j][i].size();k++)
                        {
                                vec condition;
                                condition.ins(0,string_lists[j][i][k]);
                                conditions.push_back(condition);
                                if(conditions.size()>1)
                                {
                                        conditions[k-2].ins(0,string_lists[j][i][k]);
                                }
                                if(conditions.size()>2)
                                {
                                        conditions[k-3].ins(0,string_lists[j][i][k]);
                                        //cout << conditions[k-3] << endl;// << conditions[k-3].left(1) << conditions[k-3].right(2);
                                        Ar.bayes(conditions[k-3].left(1),conditions[k-3].right(2));
                                }
                        }
                        ofstream myfile;
                        myfile.open("c:\\classic_ar1.txt",ios::app);
                        myfile << Ar.posterior().mean()[0] << ";";
                        myfile.close();
                        myfile.open("c:\\classic_ar2.txt",ios::app);
                        myfile << Ar.posterior().mean()[1] << ";";
                        myfile.close();
                }
                ofstream myfile;
                myfile.open("c:\\classic_ar1.txt",ios::app);
                myfile << endl;
                myfile.close();
                myfile.open("c:\\classic_ar2.txt",ios::app);
                myfile << endl;
                myfile.close();
        }
}

odo sort out constant terms - bayes should accept vec without additional 1s

Member Function Documentation

void bdm::ARX::from_setting ( const Setting &  set  )  [virtual]

Create object from the following structure

    class = 'ARX';
    rgr = RV({'names',...},[sizes,...],[times,...]);   % description of regressor variables
    --- optional fields ---
    prior = configuration of bdm::egiw;                % any offspring of eqiw for prior density, bdm::egiw::from_setting
    alternative = configuration of bdm::egiw;          % any offspring of eqiw for alternative density in stabilized estimation of prior density
    constant = [];                                     % 0/1 switch if the constant term is modelled or not
    --- inherited fields ---
    bdm::BMEF::from_setting
If the optional fields are not given, they will be filled as follows: 
    prior = posterior;                                % when prior is not given the posterior is used (TODO it is unclear)
    alternative = prior;                              % when alternative is not given the prior is used
    constant = 1;                                     % constant term is modelled on default

Reimplemented from bdm::BMEF.

Reimplemented in bdm::ARXg.

ivec bdm::ARX::structure_est ( const egiw &  Eg0  ) 

Brute force structure estimation.

Returns:
indices of accepted regressors.

ivec bdm::ARX::structure_est_LT ( const egiw &  Eg0  ) 

Smarter structure estimation by Ludvik Tesar.

Returns:
indices of accepted regressors.

The documentation for this class was generated from the following files:
Generated on 2 Dec 2013 for mixpp by  doxygen 1.4.7