mixpp: Introduction to Bayesian Decision Making Toolbox BDM
BDM Use - in C++

Introduction to Bayesian Decision Making Toolbox BDM

This is a brief introduction into elements used in the BDM. The toolbox was designed for two principle tasks:

  • Design of Bayesian decisions-making startegies,
  • Bayesian system identification for on-line and off-line scenarios.
Theoretically, the latter is a special case of the former, however we list it separately to highlight its importance in practical applications.

Here, we describe basic objects that are required for implementation of the Bayesian parameter estimation.

Key objects are:

Bayesian Model: class BM
which is an encapsulation of the likelihood function, the prior and methodology of evaluation of the Bayes rule. This methodology may be either exact or approximate.
Posterior density of the parameter: class epdf
representing posterior density of the parameter. Methods defined on this class allow any manipulation of the posterior, such as moment evaluation, marginalization and conditioning.

Class BM

The class BM is designed for both on-line and off-line estimation. We make the following assumptions about data:
  • an individual data record is stored in a vector, vec dt,
  • a set of data records is stored in a matrix,mat D, where each column represent one individual data record

On-line estimation is implemented by method

 void bayes(vec dt)
Off-line estimation is implemented by method
 void bayes_batch(mat D)

As an intermediate product, the bayes rule computes marginal likelihood of the data records 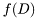$ f(D) $. Numerical value of this quantity which is important e.g. for model selection can be obtained by calling method _ll().

Getting results from BM

Class BM offers several ways how to obtain results:
  • generation of posterior or predictive pdfs, methods _epdf() and predictor()
  • direct evaluation of predictive likelihood, method logpred()
Underscore in the name of method _epdf() indicate that the method returns a pointer to the internal posterior density of the model. On the other hand, predictor creates a new structure of type epdf().

Direct evaluation of predictive pdfs via logpred offers a shortcut for more efficient implementation.

Getting results from BM

As introduced above, the results of parameter estimation are in the form of probability density function conditioned on numerical values. This type of information is represented by class epdf.

This class allows such as moment evaluation via methods mean() and variance(), marginalization via method marginal(), and conditioning via method condition().

Also, it allows generation of a sample via sample() and evaluation of one value of the posterior parameter likelihood via evallog(). Multivariate versions of these operations are also available by adding suffix _mat, i.e. sample_mat() and evallog_mat(). These methods providen multiple samples and evaluation of likelihood in multiple points respectively.

Classes for probability calculus

When a more demanding task then generation of point estimate of the parameter is required, the power of general probability claculus can be used. The following classes (together with epdf introduced above) form the basis of the calculus:
  • mpdf a pdf conditioned on another symbolic variable,
  • RV a symbolic variable on which pdfs are defined.
The former class is an extension of mpdf that allows conditioning on a symbolic variable. Hence, when numerical results - such as samples - are required, numericla values of the condition must be provided. The names of methods of the epdf are used extended by suffix cond, i.e. samplecond(), evallogcond(), where cond precedes matrix estension, i.e. samplecond_mat() and evallogcond_mat().

The latter class is used to identify how symbolic variables are to be combined together. For example, consider the task of composition of pdfs via the chain rule:

\[ f(a,b,c) = f(a|b,c) f(b) f(c) \]

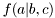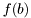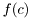In our setup, $ f(a|b,c) $ is represented by an mpdf while $ f(b) $ and $ f(c) $ by two epdfs. We need to distinguish the latter two from each other and to deside in which order they should be added to the mpdf. This distinction is facilitated by the class RV which uniquely identify a random varibale.

Therefore, each pdf keeps record on which RVs it represents; epdf needs to know only one RV stored in the attribute rv; mpdf needs to keep two RVs, one for variable on which it is defined (rv) and one for variable incondition which is stored in attribute rvc.

Generated on 2 Dec 2013 for mixpp by  doxygen 1.4.7