mixpp: BDM Use - Probability density functions

BDM Use - Probability density functions

This section serves as an introduction to basic elements of the BDM: probability density functions, pdfs.

The tutorial is written for the BDM toolbox, if you are interested in use of C++ classes see class reference pages.

Table of content:

Using built-in pdfs

In BDM toolbox, a pdf is specified by matlab structure, e.g. 
Nab.class= 'enorm<ldmat>';
Nab.mu   = [3,2];
Nab.R    = eye(2);
Nab.rv   = RV({'a','b'});
Which encodes information $ f(a,b) = \mathcal{N}(mu=[3;2],R=eye(2))$.
  • the keyword "enorm\<ldmat\>" means "Unconditional Normal distribution with covariance matrix in L'DL form", other possibilities are: "enorm\<chmat\>" for Choleski decomposition, and "enorm\<fsqmat\>" for full (non-decomposed) matrices.
  • mu denotes mean value
  • R denotes variance (written in full matrix regardles of the used decomposition),
  • parameters mu and R are vector and matrix, respectively. They can be given directly (as in Nab.mu) or as a result of arbitrary matlab function, (as in Nab.R)
  • rv denotes names assigned to the variables. RV is more complicated structure, but here it is sufficient to use default values.
  • rv is an optional parameter, some operations do not need it, such as sampling or evaluation of moments
For generating samples try: 
>> M=epdf_sample_mat(Nab,4);
which should return 4 samples of the Nab distribution.

For evaluation of mean and variance: 

>> Nab_m=epdf_mean(Nab);
>> Nab_v=epdf_variance(Nab);

Other distributions are created analogously, see ??? for their list and parameters??? Sampling and evaluation of moments are done by exactly the same functions as for the normal density.

Marginalization and conditioning

Basic operations on pdfs are marginalization and conditioning, which are provided by mex functions edpf_marginal and epdf_condition, respectively.

This operation does require the rv parametetr to be fully specified. If it isn't, it will fail with the following message 

--- fill in the message ----

If rv is correctly specified, marginal pdf of Nab on variable "a" is obtained by: 

Na = epdf_marginal(Nab,RV('a'));

Similarly for conditional: 

Na_b = epdf_condition(Nab,RV('a'));
Nb_a = epdf_condition(Nab,RV('b'));

Conditioned densities

Note that the result of conditioning is of type "mlnorm\<ldmat\>" which is a special case of pdf with variables in condition, specifically

\[ f(a|b) = \mathcal{N}(A*b+const, R)\]

i.e. "Normal distributed pdf with mean value as linear function of variable b".

This type of pdfs differ from previously used type is the way of use. For example, it is not possible to sample directly form such density, it is necessary to specify what is the value of variable in condition.

That is why a different function is used: 

Smp=pdf_samplecond_mat(Na_b, 10)

The conditioned and Unconditioned pdf may be combined together in the chain rule. The chain rule can be of two different types: conditioned or unconditioned, i.e.:

\[ f(a,b)=f(a|b)f(b), OR, f(a,b|c)=f(a|b)f(b|c)\]

Thus it is differently encoded as: 

fab.class = 'eprod';         % result is unconditioned pdf
fab.pdfs  = {fa_b, fb};
fab_c.class = 'mprod';       % result is conditioned pdf
fab_c.pdfs  = {fa_b, fb_c};

Pdfs with functional transformation

In more general type of pdfs, variables in condition may be transformed by a function. For example Gaussian density with nonlinear transformation of mean value,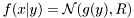 $ f(x|y) = \mathcal{N}(g(y), R)$, is represented by class mgnorm 

fx.class  = 'mgnorm<ldmat>';
fx.g      = 'mexFunction';              % function is evaluated in matlab
fx.g.function = 'test_function';         % name of the matlab function to evaluate
fx.g.dim  = 2;                          % expected dimension of output
fx.g.dimc = 2;                          % expected dimension of input
fx.R      = eye(2);                     % variance R

This example is using generic function specified by name of Matlab .m file. Compulsory fields g.dim and g.dimc are used to check correct dimension of inputs and outputs of the function.

Creating user-defined pdfs in Matlab

Definition of new pdf classes in matlab is done by extending (inheriting from) class mexPdf which is defined in file: bdmtoolbox/mex/mex_classes/mexEpdf.m

The file lists all necessary functions that must be filled in order to plug the new class into other bdm algorithms.

Please read Matlab manual for details on its implementation of object oriented programming.

For easier start, an example class, mexLaplace, is defined in <toolbox_dir>/mex/mex_classes/mexLaplace.m

Using matlab-extended classes is done via a structure with only two required fields: 

fL.class = 'mexEpdf';         % declaration of derivative from mexEpdf
fL.object = mexLaplace;       % any particular instance of mexEpdf
fL.object.mu = 1;             % set values of attributes of the chosen class, in this case mexLaplace
fL.object.b = 1;

See example bdmtoolbox/tutorial/userguide/mexpdf_example.m

For list of all available pdf objects, see bdmtoolbox - List of available basic objects

Generated on 2 Dec 2013 for mixpp by  doxygen 1.4.7