Introduction to Bayesian Decision Making Toolbox BDM

This is a brief introduction into elements used in the BDM. The toolbox was designed for two principle tasks:

Design of Bayesian decisions-making startegies,
Bayesian system identification for on-line and off-line scenarios.

Theoretically, the latter is a special case of the former, however we list it separately to highlight its importance in practical applications.

In order to achieve these principal goals in full generality, we need to implement full range of probabilistic operations such as: marginalization, conditioning, Bayes rule, combination of probability densities. Furthermore, many supportive operations are also required, such as data handling and logging of results. Here, we explain the basic classes for each task and point to advanced topics on the issue.

Philosophy of the Toolbox

The primary obstacle for creation of any any Bayesian software is how to address inherent computational intractability of the calculus. Typically, toolboxes implementing Bayesian calculus choose one particular task or one particular approximation methodology. For example, "BUGS" is a toolbox focused on evaluation using Gibbs sampling, "BNT" is focused on Bayesian Networks, "NFT" on Bayesian filtering. BDM takes another approach: all tasks are defined via their functional form, detailed implementation is an internal matter of each class.

This philosophy results in a tree structure of inheritance, where the root is an abstract class. Different approaches to Bayesian calculus are implemented as specialization of this class. Interoperability of these classes is achieved by data classes, representing mathematical objects arising in the Bayesian calculus.

The task of Bayesian estimation decribed in the next Section is a good illustration of the philosophy.

Bayesian parameter estimation

Bayesian parameter estimation is, in essence, straightforward application of the Bayes rule:

$f(\theta|D) =\frac{f(D|\theta)f(\theta)}{f(D)}$

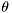where, $\theta$ is an unknown parameter, 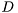$ D $ denotes the observed data, 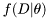$f(D|\theta)$ is the likelihood function, 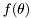$f(\theta)$ is the prior density, and 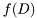$ f(D) $ is "evidence" of the data.

This simple rule has, however, many incarnations for various types of the likelihood, prior and evidence. For example, the Bayes rule can be evaluated exactly for likelihood function from the Exponential Family and conjugate prior, where the whole functional operation reduces to algebraic operation on sufficient statistics. For other likelihood functions and priors, various approximate schemes (such as Monte Carlo sampling, or maximum-likelihood optimizations) were proposed. To capture all of these options, we abstract the core functionality in the class BM:

BM, abstract class defining two key methods:

 void bayes(vec dt)

 void bayesB(mat D)

```
 epdf& _epdf(). 
```

Hence, the class represent an "estimator" that is capable of returning a posterior density (via method _epdf ) and application of the Bayes rule vis method bayes .

Functions bayes and bayesB denotes on-line and off-line scenario, respectively. Function bayes assumes that

Parameters:

	dt	is an incremental data record and applies the Bayes rule using posterior density for the previous step as a prior. On the other hand, `bayesB` assumes that
	D	is the full data record, and uses the original prior created during construction of the object.

Posterior density is represented by a class epdf . When we are interested only in part of the posterior density we can apply probability calculus via methods of this class.

Probability calculus

Key objects of probability calculus are probability density functions, pdfs. We distinguish two types of pdfs:

epdf, a pdf fully defined by statistics: $ f(a | S)$

, with numerical statics $ S $

, and mpdf, a pdf conditioned on another random variable: $ f(a| b) $

, where

is a variable.

The principal distinction between these types is that operations defined on these classes have different results. For example, the first moment of the former is a numeric value, while for the latter it is a functional form.

The most important operations on pdfs are:

evaluation in a point: implemented by methods

 double evallog(vec dt)

for epdf and

 double evallogcond()

for mpdf. marginalization: implemented by method

 epdf* marginal(RV rv)

for epdf, conditioning: implemented by method

 mpdf* conditional(RV rv)

for epdf.

Note that a new data class, RV, is introduced. This class represents description of a multivariate random variable.

Random Variables

In mathematics, variable is a symbol of quantity that has no assigned value. Its purpose is to distinguish one variable from another. Hence, in software representation it has a meaning of unique identifier. Since we allow multivariate random variables, the variable also carries its dimensionality. Moreover, for dealing with time-varying estimation it also makes sense to distinguish different time-shift of variables.

The main purpose of this class is to mediate composition and decomposition of pdfs. See,...