eDirich Class Reference
Dirichlet posterior density. More...
#include <libEF.h>
Inheritance diagram for eDirich:

Collaboration diagram for eDirich:
Public Member Functions | |
| eDirich (const RV &rv, const vec &beta0) | |
| Default constructor. | |
| eDirich (const eDirich &D0) | |
| Copy constructor. | |
| vec | sample () const |
Returns a sample, 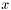 from density from density 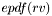 . . | |
| vec | mean () const |
| return expected value | |
| vec | variance () const |
| return expected variance (not covariance!) | |
| double | evallog_nn (const vec &val) const |
| In this instance, val is ... | |
| double | lognc () const |
logarithm of the normalizing constant,  | |
| vec & | _beta () |
| access function | |
| void | set_parameters (const vec &beta0) |
| Set internal parameters. | |
| virtual void | dupdate (mat &v) |
| TODO decide if it is really needed. | |
| virtual double | evallog (const vec &val) const |
| Evaluate normalized log-probability. | |
| virtual vec | evallog (const mat &Val) const |
| Evaluate normalized log-probability for many samples. | |
| virtual void | pow (double p) |
| Power of the density, used e.g. to flatten the density. | |
| virtual mat | sample_m (int N) const |
Returns N samples from density 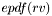 . . | |
| virtual vec | evallog_m (const mat &Val) const |
Compute log-probability of multiple values argument val. | |
| virtual mpdf * | condition (const RV &rv) const |
| Return conditional density on the given RV, the remaining rvs will be in conditioning. | |
| virtual epdf * | marginal (const RV &rv) const |
| Return marginal density on the given RV, the remainig rvs are intergrated out. | |
| const RV & | _rv () const |
| access function, possibly dangerous! | |
| void | _renewrv (const RV &in_rv) |
| modifier function - useful when copying epdfs | |
Protected Attributes | |
| vec | beta |
| sufficient statistics | |
| double | gamma |
| speedup variable | |
| RV | rv |
| Identified of the random variable. | |
Detailed Description
Dirichlet posterior density.
Continuous Dirichlet density of 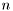 -dimensional variable
-dimensional variable 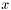
![\[ f(x|\beta) = \frac{\Gamma[\gamma]}{\prod_{i=1}^{n}\Gamma(\beta_i)} \prod_{i=1}^{n}x_i^{\beta_i-1} \]](form_76.png)
where 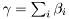 .
.
The documentation for this class was generated from the following file:
- work/git/mixpp/bdm/stat/libEF.h
 1.5.6
1.5.6