bdm::migamma_fix Class Reference
Inverse-Gamma random walk around a fixed point. More...
#include <libEF.h>
Public Member Functions | |
| migamma_fix (const RV &rv, const RV &rvc) | |
| Constructor. | |
| void | set_parameters (double k0, vec ref0, double l0) |
Set value of k. | |
| void | condition (const vec &val) |
Update ep so that it represents this mpdf conditioned on rvc = cond. | |
| void | set_parameters (double k0) |
Set value of k. | |
| virtual vec | samplecond (const vec &cond, double &ll) |
Returns a sample from the density conditioned on cond, 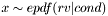 . . | |
| virtual mat | samplecond_m (const vec &cond, vec &ll, int N) |
| Returns. | |
| virtual double | evallogcond (const vec &dt, const vec &cond) |
| Shortcut for conditioning and evaluation of the internal epdf. In some cases, this operation can be implemented efficiently. | |
| virtual vec | evallogcond_m (const mat &Dt, const vec &cond) |
| Matrix version of evallogcond. | |
| RV | _rvc () const |
| access function | |
| RV | _rv () const |
| access function | |
| epdf & | _epdf () |
| access function | |
| epdf * | _e () |
| access function | |
Protected Attributes | |
| double | l |
| parameter l | |
| vec | refl |
| reference vector | |
| eigamma | epdf |
Internal epdf that arise by conditioning on rvc. | |
| double | k |
Constant 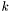 . . | |
| vec * | _beta |
| cache of epdf.beta | |
| vec * | _alpha |
| chaceh of epdf.alpha | |
| RV | rv |
| modeled random variable | |
| RV | rvc |
| random variable in condition | |
| epdf * | ep |
| pointer to internal epdf | |
Detailed Description
Inverse-Gamma random walk around a fixed point.
Mean value, 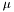 , of this density is given by a geometric combination of
, of this density is given by a geometric combination of rvc and given fixed point, 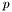 .
. 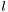 is the coefficient of the geometric combimation
is the coefficient of the geometric combimation
![\[ \mu = \mu_{t-1} ^{l} p^{1-l}\]](form_18.png)
==== Check == vv = Standard deviation of the random walk is proportional to one 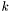 -th the mean. This is achieved by setting
-th the mean. This is achieved by setting 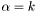 and
and 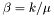 .
.
The standard deviation of the walk is then: 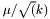 .
.
Member Function Documentation
| virtual vec bdm::mpdf::samplecond | ( | const vec & | cond, | |
| double & | ll | |||
| ) | [inline, virtual, inherited] |
Returns a sample from the density conditioned on cond, 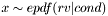 .
.
- Parameters:
-
cond is numeric value of rvll is a return value of log-likelihood of the sample.
Reimplemented in bdm::mprod.
References bdm::mpdf::condition(), bdm::mpdf::ep, bdm::epdf::evallog(), and bdm::epdf::sample().
Referenced by bdm::MPF< BM_T >::bayes(), bdm::PF::bayes(), and bdm::ArxDS::step().
| virtual mat bdm::mpdf::samplecond_m | ( | const vec & | cond, | |
| vec & | ll, | |||
| int | N | |||
| ) | [inline, virtual, inherited] |
Returns.
- Parameters:
-
N samples from the density conditioned on cond,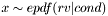 .
. cond is numeric value of rvll is a return value of log-likelihood of the sample.
References bdm::mpdf::condition(), bdm::RV::count(), bdm::mpdf::ep, bdm::epdf::evallog(), bdm::mpdf::rv, and bdm::epdf::sample().
The documentation for this class was generated from the following file:
 1.5.6
1.5.6