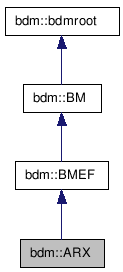
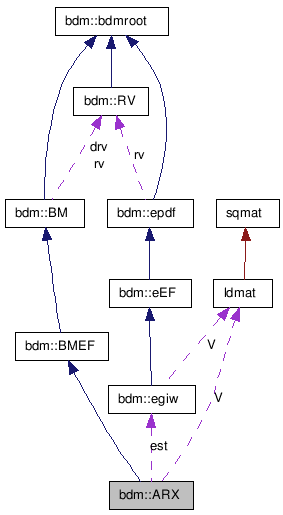
bdm::ARX Class Reference
Linear Autoregressive model with Gaussian noise. More...
#include <arx.h>
Public Member Functions | |
| ARX (const RV &rv, const mat &V0, const double &nu0, const double frg0=1.0) | |
| Full constructor. | |
| ARX (const ARX &A0) | |
| Copy constructor. | |
| ARX * | _copy_ (bool changerv=false) |
| Auxiliary function. | |
| void | set_parameters (const ldmat &V0, const double &nu0) |
| Set sufficient statistics. | |
| void | set_statistics (const BMEF *BM0) |
| get statistics from another model | |
| void | get_parameters (mat &V0, double &nu0) |
| Returns sufficient statistics. | |
| void | bayes (const vec &dt, const double w) |
Here ![$dt = [y_t psi_t] $](form_58.png) . . | |
| void | bayes (const vec &dt) |
| Incremental Bayes rule. | |
| const epdf & | _epdf () const |
| Returns a reference to the epdf representing posterior density on parameters. | |
| double | logpred (const vec &dt) const |
| void | flatten (const BMEF *B) |
| Flatten the posterior according to the given BMEF (of the same type!). | |
| enorm< ldmat > * | predictor (const RV &rv0, const vec &rgr) const |
| Conditioned version of the predictor. | |
| enorm< ldmat > * | predictor (const RV &rv0) const |
| Constructs a predictive density (marginal density on data). | |
| mlnorm< ldmat > * | predictor (const RV &rv0, const RV &rvc0) const |
| conditional version of the predictor | |
| mlstudent * | predictor_student (const RV &rv0, const RV &rvc0) const |
| ivec | structure_est (egiw Eg0) |
| Brute force structure estimation. | |
| const egiw * | _e () const |
| Returns a pointer to the epdf representing posterior density on parameters. Use with care! | |
| virtual void | bayesB (const mat &Dt) |
| Batch Bayes rule (columns of Dt are observations). | |
| vec | logpred_m (const mat &dt) const |
| Matrix version of logpred. | |
| const RV & | _rv () const |
| access function | |
| const RV & | _drv () const |
| access function | |
| void | set_drv (const RV &rv) |
| set drv | |
| double | _ll () const |
| access function | |
| void | set_evalll (bool evl0) |
| access function | |
Protected Attributes | |
| egiw | est |
Posterior estimate of 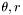 in the form of Normal-inverse Wishart density. in the form of Normal-inverse Wishart density. | |
| ldmat & | V |
| cached value of est.V | |
| double & | nu |
| cached value of est.nu | |
| double | frg |
| forgetting factor | |
| double | last_lognc |
cached value of lognc() in the previous step (used in evaluation of ll ) | |
| RV | rv |
| Random variable of the posterior. | |
| RV | drv |
| Random variable of the data (optional). | |
| double | ll |
| Logarithm of marginalized data likelihood. | |
| bool | evalll |
If true, the filter will compute likelihood of the data record and store it in ll . Set to false if you want to save computational time. | |
Detailed Description
Linear Autoregressive model with Gaussian noise.Regression of the following kind:
![\[ y_t = \theta_1 \psi_1 + \theta_2 + \psi_2 +\ldots + \theta_n \psi_n + r e_t \]](form_61.png)
where unknown parameters rv are ![$[\theta r]$](form_51.png) , regression vector
, regression vector 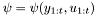 is a known function of past outputs and exogeneous variables
is a known function of past outputs and exogeneous variables 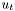 . Distrubances
. Distrubances 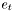 are supposed to be normally distributed:
are supposed to be normally distributed:
![\[ e_t \sim \mathcal{N}(0,1). \]](form_62.png)
Extension for time-variant parameters 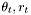 may be achived using exponential forgetting (Kulhavy and Zarrop, 1993). In such a case, the forgetting factor
may be achived using exponential forgetting (Kulhavy and Zarrop, 1993). In such a case, the forgetting factor frg 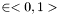 should be given in the constructor. Time-invariant parameters are estimated for
should be given in the constructor. Time-invariant parameters are estimated for frg = 1.
Member Function Documentation
| void bdm::ARX::bayes | ( | const vec & | dt | ) | [inline, virtual] |
| double bdm::ARX::logpred | ( | const vec & | dt | ) | const [virtual] |
Evaluates predictive log-likelihood of the given data record I.e. marginal likelihood of the data with the posterior integrated out.
Reimplemented from bdm::BM.
References bdm::egiw::_nu(), bdm::egiw::_V(), est, bdm::BM::evalll, bdm::BMEF::frg, bdm::BMEF::last_lognc, bdm::egiw::lognc(), nu, ldmat::opupdt(), bdm::egiw::pow(), and V.
| ivec bdm::ARX::structure_est | ( | egiw | Eg0 | ) |
Brute force structure estimation.
- Returns:
- indeces of accepted regressors.
References bdm::RV::count(), bdm::egiw_bestbelow(), est, and bdm::egiw::lognc().
The documentation for this class was generated from the following files:
- arx.h
- bdm/estim/arx.cpp
 1.5.6
1.5.6