bdm::eprod Class Reference

#include <emix.h>

Inheritance diagram for bdm::eprod:

List of all members.

---

Detailed Description

Product of independent epdfs. For dependent pdfs, use mprod.

Public Member Functions
	eprod (const Array< const epdf * > epdfs0)
vec	mean () const
	return expected value
vec	variance () const
	return expected variance (not covariance!)
vec	sample () const
	Returns a sample, from density .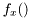
double	evallog (const vec &val) const
	Compute log-probability of argument val.
const epdf *	operator() (int i) const
	access function
	~eprod ()
	Destructor.
Constructors
Construction of each epdf should support two types of constructors: empty constructor, copy constructor, The following constructors should be supported for convenience: constructor followed by calling set_parameters() constructor accepting random variables calling set_rv() All internal data structures are constructed as empty. Their values (including sizes) will be set by method set_parameters(). This way references can be initialized in constructors.
void	set_parameters (int dim0)
Matematical Operations
virtual mat	sample_m (int N) const
	Returns N samples, from density .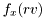
virtual vec	evallog_m (const mat &Val) const
	Compute log-probability of multiple values argument val.
virtual mpdf *	condition (const RV &rv) const
	Return conditional density on the given RV, the remaining rvs will be in conditioning.
virtual epdf *	marginal (const RV &rv) const
	Return marginal density on the given RV, the remainig rvs are intergrated out.
virtual void	qbounds (vec &lb, vec &ub, double percentage=0.95) const
	Lower and upper bounds of percentage % quantile, returns mean-2*sigma as default.
Connection to other classes
Description of the random quantity via attribute rv is optional. For operations such as sampling rv does not need to be set. However, for marginalization and conditioning rv has to be set. NB:
void	set_rv (const RV &rv0)
	Name its rv.
bool	isnamed () const
	True if rv is assigned.
const RV &	_rv () const
	Return name (fails when isnamed is false).
Access to attributes
int	dimension () const
	Size of the random variable.
Protected Attributes
Array< const epdf * >	epdfs
	Components (epdfs).
Array< datalink * >	dls
	Array of indeces.
int	dim
	dimension of the random variable
RV	rv
	Description of the random variable.

---

The documentation for this class was generated from the following file:

• emix.h