Channel Modeling
[Communications Module]
Communication Channel Models.
More...
Classes | |
| class | itpp::Fading_Generator |
| Fading generator class. More... | |
| class | itpp::Independent_Fading_Generator |
| Independent (random) fading generator class. More... | |
| class | itpp::Static_Fading_Generator |
| Static fading generator class. More... | |
| class | itpp::Correlated_Fading_Generator |
| Correlated (random) fading generator class. More... | |
| class | itpp::Rice_Fading_Generator |
| Rice type fading generator class. More... | |
| class | itpp::FIR_Fading_Generator |
| FIR type Fading generator class. More... | |
| class | itpp::IFFT_Fading_Generator |
| IFFT type Fading generator class. More... | |
| class | itpp::Channel_Specification |
| General specification of a time-domain multipath channel. More... | |
| class | itpp::TDL_Channel |
| Tapped Delay Line (TDL) channel model. More... | |
| class | itpp::BSC |
| A Binary Symetric Channel with crossover probability p. More... | |
| class | itpp::AWGN_Channel |
| Ordinary AWGN Channel for cvec or vec inputs and outputs. More... | |
Enumerations | |
| enum | itpp::CHANNEL_PROFILE { ITU_Vehicular_A, ITU_Vehicular_B, ITU_Pedestrian_A, ITU_Pedestrian_B, COST207_RA, COST207_RA6, COST207_TU, COST207_TU6alt, COST207_TU12, COST207_TU12alt, COST207_BU, COST207_BU6alt, COST207_BU12, COST207_BU12alt, COST207_HT, COST207_HT6alt, COST207_HT12, COST207_HT12alt, COST259_TUx, COST259_RAx, COST259_HTx } |
| Predefined channel profiles. Includes LOS and Doppler spectrum settings. | |
| enum | itpp::FADING_TYPE { Independent, Static, Correlated } |
| Fading generator type: Independent (default), Static or Correlated. | |
| enum | itpp::CORRELATED_METHOD { Rice_MEDS, IFFT, FIR } |
| Correlated fading generation methods: Rice_MEDS (default), IFFT or FIR. | |
| enum | itpp::RICE_METHOD { MEDS } |
| Rice fading generation methods: MEDS. | |
| enum | itpp::DOPPLER_SPECTRUM { Jakes = 0, J = 0, Classic = 0, C = 0, GaussI = 1, Gauss1 = 1, GI = 1, G1 = 1, GaussII = 2, Gauss2 = 2, GII = 2, G2 = 2 } |
| Predefined Doppler spectra. | |
Detailed Description
Communication Channel Models.
Table of Contents
Introduction
When simulating a communication link, a model of the channel behaviour is usually needed. Such a model typically consist of three parts: the propagation attenuation, the shadowing (log-normal fading) and the multipath fading (small scale fading). In the following we will focus on the small scale (or multipath) fading.
Multipath fading is the process where the received signal is a sum of many reflections, each with different propagation time, phase and attenuation. The sum signal will vary in time if the receiver (or transmitter) moves, or if some of the reflectors move. We usually refer to this process as a fading process and try to model it as a stochastic process. The most common model is the Rayleigh fading model where the process is modeled as a sum of infinitely many (in practise it is enough with only a few) received reflections from all angles (uniformly distributed) around the receiver. Mathematically we write the received signal, 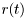 as
as
![\[ r(t) = a(t) * s(t), \]](form_190.png)
where 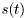 is the transmitted signal and
is the transmitted signal and 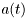 is the complex channel coefficient (or fading process). If this process is modeled as a Rayleigh fading process then
is the complex channel coefficient (or fading process). If this process is modeled as a Rayleigh fading process then 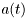 is a complex Gaussian process and the envelope
is a complex Gaussian process and the envelope 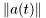 is Rayleigh distributed.
is Rayleigh distributed.
Doppler
The speed by which the channel changes is decided by the speed of the mobile (transmitter or receiver or both). This movement will cause the channel coefficient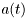 to be correlated in time (or equivalently in frequency). Different models of this correlation exist, but the most common is the classical Jakes model where the correlation function is given as
to be correlated in time (or equivalently in frequency). Different models of this correlation exist, but the most common is the classical Jakes model where the correlation function is given as
![\[ R(\tau) = E[a^*(t) a(t+\tau)] = J_0(2 \pi f_\mathrm{max} \tau), \]](form_194.png)
where 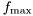 is the maximum Doppler frequency given by
is the maximum Doppler frequency given by
![\[ f_\mathrm{max} = \frac{v}{\lambda} = \frac{v}{c_0} f_c. \]](form_196.png)
Here 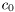 is the speed of light and
is the speed of light and 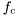 is the carrier frequency. Often the maximum Doppler frequency is given as the normalized Doppler
is the carrier frequency. Often the maximum Doppler frequency is given as the normalized Doppler 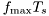 , where
, where 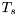 is the sample duration (often the symbol time) of the simulated system. Instead of specifying the correlation function
is the sample duration (often the symbol time) of the simulated system. Instead of specifying the correlation function 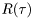 one can specify the Doppler spectrum (the Fourier transform of
one can specify the Doppler spectrum (the Fourier transform of 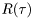 ).
).
Frequency-selective Channels
Since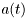 affects the transmitted signal as a constant scaling factor at a given time, this channel model is often referred to as flat-fading (or frequency non-selective fading). On the other hand, if time arrivals of the reflections are very different (compared to the sampling time), we cannot model the received signal only as a scaled version of the transmitted signal. Instead we model the channel as frequency-selective but time-invariant (or at least wide-sense stationary) with the impulse response
affects the transmitted signal as a constant scaling factor at a given time, this channel model is often referred to as flat-fading (or frequency non-selective fading). On the other hand, if time arrivals of the reflections are very different (compared to the sampling time), we cannot model the received signal only as a scaled version of the transmitted signal. Instead we model the channel as frequency-selective but time-invariant (or at least wide-sense stationary) with the impulse response
![\[ h(t) = \sum_{k=0}^{N_\mathrm{taps}-1} a_k \exp (-j \theta_k ) \delta(t-\tau_k), \]](form_202.png)
where 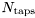 is the number of channel taps,
is the number of channel taps, 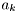 is the average amplitude at delay
is the average amplitude at delay 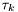 , and
, and 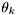 is the channel phase of the
is the channel phase of the 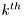 channel tap.
channel tap.
The average power and delay profiles are defined as:
![\[ \mathbf{a} = [a_0, a_1, \ldots, a_{N_\mathrm{taps}-1}] \]](form_208.png)
and
![\[ \mathbf{\tau} = [\tau_0, \tau_1, \ldots, \tau_{N_\mathrm{taps}-1}], \]](form_209.png)
respectively. We assume without loss of generality that 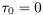 and
and 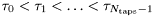 . Now the received signal is simply a linear filtering (or convolution) of the transmitted signal, where
. Now the received signal is simply a linear filtering (or convolution) of the transmitted signal, where 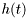 is the impulse response of the filter.
is the impulse response of the filter.
In practice, when simulating a communication link, the impulse response 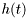 is sampled with a sample period
is sampled with a sample period 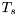 that is related to the symbol rate of the system of investigation (often 2-8 times higher). Hence, the impulse response of the channel can now be modeled as a time-discrete filter or tapped-delay line (TDL) where the delays are given as
that is related to the symbol rate of the system of investigation (often 2-8 times higher). Hence, the impulse response of the channel can now be modeled as a time-discrete filter or tapped-delay line (TDL) where the delays are given as 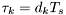 , and
, and 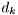 are positive integers.
are positive integers.
Line of Sight (LOS) or Rice Fading
If there is a line of sight (LOS) between the transmitter and receiver the first component received (or a few first) will have a static component that depends only on the Doppler frequency. In practice the difference in time between the first LOS component(s) and the reflected components is small and hence in a discretized system the first tap is usually modeled as a LOS component and a fading component. Such a process is usually called a Rice fading process.The LOS component can be expressed as:
![\[ \rho \exp(2 \pi f_\rho t + \theta_\rho), \]](form_215.png)
where 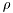 ,
, 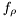 , and
, and 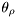 are the amplitude, Doppler frequency and phase of the LOS component, respectively. Instead of stating the amplitude itself, the ratio of the LOS power and total fading process power, called the Rice factor (or relative power), is often used. The Doppler frequency is limited by the maximum Doppler frequency
are the amplitude, Doppler frequency and phase of the LOS component, respectively. Instead of stating the amplitude itself, the ratio of the LOS power and total fading process power, called the Rice factor (or relative power), is often used. The Doppler frequency is limited by the maximum Doppler frequency 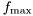 and hence typically the Doppler of the LOS is expressed relative to its maximum (common is
and hence typically the Doppler of the LOS is expressed relative to its maximum (common is 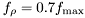 ). The phase is usually assumed to be random and can without loss of generality be set to 0 (does not affect the statistics of the process).
). The phase is usually assumed to be random and can without loss of generality be set to 0 (does not affect the statistics of the process).
References
- [Pat02] Matthias Patzold, Mobile fading channels, Wiley, 2002.
- [Stu01] Gordon L. Stuber, Principles of mobile communication, 2nd. ed., Kluwer, 2001.
- [Rap96] Theodore S. Rappaport, Wireless communications: principles and practise, Prentice Hall, 1996.
 1.5.8
1.5.8