Miscellaneous Statistics Functions
[Statistics Module]
Classes | |
| class | itpp::Stat |
| A class for sampling a signal and calculating statistics. More... | |
Functions | |
| double | itpp::mean (const vec &v) |
| The mean value. | |
| std::complex< double > | itpp::mean (const cvec &v) |
| The mean value. | |
| double | itpp::mean (const svec &v) |
| The mean value. | |
| double | itpp::mean (const ivec &v) |
| The mean value. | |
| double | itpp::mean (const mat &m) |
| The mean value. | |
| std::complex< double > | itpp::mean (const cmat &m) |
| The mean value. | |
| double | itpp::mean (const smat &m) |
| The mean value. | |
| double | itpp::mean (const imat &m) |
| The mean value. | |
| template<class T > | |
| double | itpp::geometric_mean (const Vec< T > &v) |
| The geometric mean of a vector. | |
| template<class T > | |
| double | itpp::geometric_mean (const Mat< T > &m) |
| The geometric mean of a matrix. | |
| template<class T > | |
| double | itpp::median (const Vec< T > &v) |
| The median. | |
| double | itpp::norm (const cvec &v) |
| Calculate the 2-norm: norm(v)=sqrt(sum(abs(v).^2)). | |
| template<class T > | |
| double | itpp::norm (const Vec< T > &v) |
| Calculate the 2-norm: norm(v)=sqrt(sum(abs(v).^2)). | |
| double | itpp::norm (const cvec &v, int p) |
| Calculate the p-norm: norm(v,p)=sum(abs(v).^2)^(1/p). | |
| template<class T > | |
| double | itpp::norm (const Vec< T > &v, int p) |
| Calculate the p-norm: norm(v,p)=sum(abs(v).^2)^(1/p). | |
| double | itpp::norm (const cvec &v, const std::string &s) |
| Calculate the Frobenius norm for s = "fro" (equal to 2-norm). | |
| template<class T > | |
| double | itpp::norm (const Vec< T > &v, const std::string &s) |
| Calculate the Frobenius norm for s = "fro" (equal to 2-norm). | |
| double | itpp::norm (const mat &m, int p) |
| double | itpp::norm (const cmat &m, int p) |
| double | itpp::norm (const mat &m, const std::string &s) |
| Calculate the Frobenius norm of a matrix for s = "fro". | |
| double | itpp::norm (const cmat &m, const std::string &s) |
| Calculate the Frobenius norm of a matrix for s = "fro". | |
| double | itpp::variance (const cvec &v) |
| The variance of the elements in the vector. Normalized with N-1 to be unbiased. | |
| template<class T > | |
| double | itpp::variance (const Vec< T > &v) |
| The variance of the elements in the vector. Normalized with N-1 to be unbiased. | |
| template<class T > | |
| double | itpp::energy (const Vec< T > &v) |
| Calculate the energy: squared 2-norm. energy(v)=sum(abs(v).^2). | |
| bool | itpp::within_tolerance (double x, double xref, double tol=1e-14) |
Return true if the input value x is within the tolerance tol of the reference value xref. | |
| bool | itpp::within_tolerance (std::complex< double > x, std::complex< double > xref, double tol=1e-14) |
Return true if the input value x is within the tolerance tol of the reference value xref. | |
| bool | itpp::within_tolerance (const vec &x, const vec &xref, double tol=1e-14) |
Return true if the input vector x is elementwise within the tolerance tol of the reference vector xref. | |
| bool | itpp::within_tolerance (const cvec &x, const cvec &xref, double tol=1e-14) |
Return true if the input vector x is elementwise within the tolerance tol of the reference vector xref. | |
| bool | itpp::within_tolerance (const mat &X, const mat &Xref, double tol=1e-14) |
Return true if the input matrix X is elementwise within the tolerance tol of the reference matrix Xref. | |
| bool | itpp::within_tolerance (const cmat &X, const cmat &Xref, double tol=1e-14) |
Return true if the input matrix X is elementwise within the tolerance tol of the reference matrix Xref. | |
| double | itpp::moment (const vec &x, const int r) |
| Calculate the central moment of vector x. | |
| double | itpp::skewness (const vec &x) |
| Calculate the skewness excess of the input vector x. | |
| double | itpp::kurtosisexcess (const vec &x) |
| Calculate the kurtosis excess of the input vector x. | |
| double | itpp::kurtosis (const vec &x) |
| Calculate the kurtosis of the input vector x. | |
Function Documentation
| double itpp::kurtosis | ( | const vec & | x | ) | [inline] |
Calculate the kurtosis of the input vector x.
The kurtosis is a measure of peakedness of a distribution. The kurtosis is defined as
![\[ \gamma_2 = \frac{\mathrm{E}[x-\mu]^4}{\sigma^4} \]](form_387.png)
where 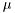 is the mean and
is the mean and 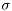 the standard deviation. For a Gaussian variable, the kurtusis is 3.
the standard deviation. For a Gaussian variable, the kurtusis is 3.
See also the definition of kurtosisexcess.
References itpp::kurtosisexcess().
| double itpp::kurtosisexcess | ( | const vec & | x | ) |
Calculate the kurtosis excess of the input vector x.
The kurtosis excess is a measure of peakedness of a distribution. The kurtosis excess is defined as
![\[ \gamma_2 = \frac{\mathrm{E}[x-\mu]^4}{\sigma^4} - 3 \]](form_383.png)
where 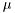 is the mean and
is the mean and 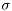 the standard deviation.
the standard deviation.
The kurtosis excess is estimated as
![\[ \gamma_2 = \frac{k_4}{{k_2}^2} \]](form_384.png)
where
![\[ k_2 = \frac{n}{n-1} m_2 \]](form_379.png)
and
![\[ k_4 = \frac{n^2 [(n+1)m_4 - 3(n-1){m_2}^2]}{(n-1)(n-2)(n-3)} \]](form_385.png)
Here  is the sample variance and
is the sample variance and 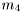 is the 4th sample central moment.
is the 4th sample central moment.
References itpp::moment(), and itpp::variance().
Referenced by itpp::kurtosis().
| double itpp::moment | ( | const vec & | x, | |
| const int | r | |||
| ) |
Calculate the central moment of vector x.
The 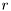 th sample central moment of the samples in the vector
th sample central moment of the samples in the vector  is defined as
is defined as
![\[ m_r = \mathrm{E}[x-\mu]^r = \frac{1}{n} \sum_{i=0}^{n-1} (x_i - \mu)^r \]](form_375.png)
where 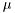 is the sample mean.
is the sample mean.
References itpp::mean(), and itpp::pow().
Referenced by itpp::kurtosisexcess(), and itpp::skewness().
| double itpp::norm | ( | const cmat & | m, | |
| int | p = 2 | |||
| ) |
Calculate the p-norm of a complex matrix
p = 1: max(svd(m)) p = 2: max(sum(abs(X)))
Default if no p is given is the 2-norm
References itpp::abs(), it_assert, itpp::max(), itpp::sum(), and itpp::svd().
| double itpp::norm | ( | const mat & | m, | |
| int | p = 2 | |||
| ) |
Calculate the p-norm of a real matrix
p = 1: max(svd(m)) p = 2: max(sum(abs(X)))
Default if no p is given is the 2-norm
References itpp::abs(), it_assert, itpp::max(), itpp::sum(), and itpp::svd().
| double itpp::skewness | ( | const vec & | x | ) |
Calculate the skewness excess of the input vector x.
The skewness is a measure of the degree of asymmetry of distribution. Negative skewness means that the distribution is spread more to the left of the mean than to the right, and vice versa if the skewness is positive.
The skewness of the samples in the vector  is
is
![\[ \gamma_1 = \frac{\mathrm{E}[x-\mu]^3}{\sigma^3} \]](form_376.png)
where 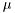 is the mean and
is the mean and 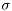 the standard deviation.
the standard deviation.
The skewness is estimated as
![\[ \gamma_1 = \frac{k_3}{{k_2}^{3/2}} \]](form_378.png)
where
![\[ k_2 = \frac{n}{n-1} m_2 \]](form_379.png)
and
![\[ k_3 = \frac{n^2}{(n-1)(n-2)} m_3 \]](form_380.png)
Here  is the sample variance and
is the sample variance and  is the 3rd sample central moment.
is the 3rd sample central moment.
References itpp::moment(), itpp::pow(), and itpp::variance().
 1.5.8
1.5.8