Matrix Decompositions
[Linear Algebra]
Functions | |
| bool | itpp::chol (const mat &X, mat &F) |
| Cholesky factorisation of real symmetric and positive definite matrix. | |
| mat | itpp::chol (const mat &X) |
| Cholesky factorisation of real symmetric and positive definite matrix. | |
| bool | itpp::chol (const cmat &X, cmat &F) |
| Cholesky factorisation of complex hermitian and positive-definite matrix. | |
| cmat | itpp::chol (const cmat &X) |
| Cholesky factorisation of complex hermitian and positive-definite matrix. | |
| bool | itpp::eig_sym (const mat &A, vec &d, mat &V) |
| Calculates the eigenvalues and eigenvectors of a symmetric real matrix. | |
| bool | itpp::eig_sym (const mat &A, vec &d) |
| Calculates the eigenvalues of a symmetric real matrix. | |
| vec | itpp::eig_sym (const mat &A) |
| Calculates the eigenvalues of a symmetric real matrix. | |
| bool | itpp::eig_sym (const cmat &A, vec &d, cmat &V) |
| Calculates the eigenvalues and eigenvectors of a hermitian complex matrix. | |
| bool | itpp::eig_sym (const cmat &A, vec &d) |
| Calculates the eigenvalues of a hermitian complex matrix. | |
| vec | itpp::eig_sym (const cmat &A) |
| Calculates the eigenvalues of a hermitian complex matrix. | |
| bool | itpp::eig (const mat &A, cvec &d, cmat &V) |
| Calculates the eigenvalues and eigenvectors of a real non-symmetric matrix. | |
| bool | itpp::eig (const mat &A, cvec &d) |
| Calculates the eigenvalues of a real non-symmetric matrix. | |
| cvec | itpp::eig (const mat &A) |
| Calculates the eigenvalues of a real non-symmetric matrix. | |
| bool | itpp::eig (const cmat &A, cvec &d, cmat &V) |
| Calculates the eigenvalues and eigenvectors of a complex non-hermitian matrix. | |
| bool | itpp::eig (const cmat &A, cvec &d) |
| Calculates the eigenvalues of a complex non-hermitian matrix. | |
| cvec | itpp::eig (const cmat &A) |
| Calculates the eigenvalues of a complex non-hermitian matrix. | |
| bool | itpp::lu (const mat &X, mat &L, mat &U, ivec &p) |
| LU factorisation of real matrix. | |
| bool | itpp::lu (const cmat &X, cmat &L, cmat &U, ivec &p) |
| LU factorisation of real matrix. | |
| void | itpp::interchange_permutations (vec &b, const ivec &p) |
| Makes swapping of vector b according to the interchange permutation vector p. | |
| bmat | itpp::permutation_matrix (const ivec &p) |
| Make permutation matrix P from the interchange permutation vector p. | |
| bool | itpp::qr (const mat &A, mat &Q, mat &R) |
| QR factorisation of real matrix. | |
| bool | itpp::qr (const mat &A, mat &R) |
| QR factorisation of real matrix with suppressed evaluation of Q. | |
| bool | itpp::qr (const mat &A, mat &Q, mat &R, bmat &P) |
| QR factorisation of real matrix with pivoting. | |
| bool | itpp::qr (const cmat &A, cmat &Q, cmat &R) |
| QR factorisation of a complex matrix. | |
| bool | itpp::qr (const cmat &A, cmat &R) |
| QR factorisation of complex matrix with suppressed evaluation of Q. | |
| bool | itpp::qr (const cmat &A, cmat &Q, cmat &R, bmat &P) |
| QR factorisation of a complex matrix with pivoting. | |
| bool | itpp::schur (const mat &A, mat &U, mat &T) |
| Schur decomposition of a real matrix. | |
| mat | itpp::schur (const mat &A) |
| Schur decomposition of a real matrix. | |
| bool | itpp::schur (const cmat &A, cmat &U, cmat &T) |
| Schur decomposition of a complex matrix. | |
| cmat | itpp::schur (const cmat &A) |
| Schur decomposition of a complex matrix. | |
| bool | itpp::svd (const mat &A, vec &s) |
Get singular values s of a real matrix A using SVD. | |
| bool | itpp::svd (const cmat &A, vec &s) |
Get singular values s of a complex matrix A using SVD. | |
| vec | itpp::svd (const mat &A) |
Return singular values of a real matrix A using SVD. | |
| vec | itpp::svd (const cmat &A) |
Return singular values of a complex matrix A using SVD. | |
| bool | itpp::svd (const mat &A, mat &U, vec &s, mat &V) |
Perform Singular Value Decomposition (SVD) of a real matrix A. | |
| bool | itpp::svd (const cmat &A, cmat &U, vec &s, cmat &V) |
Perform Singular Value Decomposition (SVD) of a complex matrix A. | |
Function Documentation
Cholesky factorisation of complex hermitian and positive-definite matrix.
The Cholesky factorisation of a hermitian positive-definite matrix 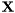 of size
of size  is given by
is given by
![\[ \mathbf{X} = \mathbf{F}^H \mathbf{F} \]](form_129.png)
where 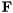 is an upper triangular
is an upper triangular  matrix.
matrix.
References itpp::chol(), and it_warning.
Cholesky factorisation of complex hermitian and positive-definite matrix.
The Cholesky factorisation of a hermitian positive-definite matrix 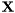 of size
of size  is given by
is given by
![\[ \mathbf{X} = \mathbf{F}^H \mathbf{F} \]](form_129.png)
where 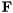 is an upper triangular
is an upper triangular  matrix.
matrix.
Returns true if calculation succeeded. False otherwise.
If X is positive definite, true is returned and F=chol(X) produces an upper triangular F. If also X is symmetric then F'*F = X. If X is not positive definite, false is returned.
References it_error.
Cholesky factorisation of real symmetric and positive definite matrix.
The Cholesky factorisation of a real symmetric positive-definite matrix 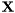 of size
of size  is given by
is given by
![\[ \mathbf{X} = \mathbf{F}^T \mathbf{F} \]](form_127.png)
where 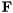 is an upper triangular
is an upper triangular  matrix.
matrix.
References it_warning.
Referenced by chmat::chmat(), itpp::chol(), ldmat::ldmat(), and fsqmat::sqrt_mult().
Cholesky factorisation of real symmetric and positive definite matrix.
The Cholesky factorisation of a real symmetric positive-definite matrix 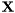 of size
of size  is given by
is given by
![\[ \mathbf{X} = \mathbf{F}^T \mathbf{F} \]](form_127.png)
where 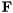 is an upper triangular
is an upper triangular  matrix.
matrix.
Returns true if calculation succeeded. False otherwise.
References it_error.
Calculates the eigenvalues of a complex non-hermitian matrix.
The Eigenvalues 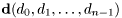 and the eigenvectors
and the eigenvectors 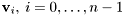 of the complex
of the complex  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
Uses the LAPACK routine ZGEEV.
Referenced by itpp::eig(), and itpp::roots().
Calculates the eigenvalues of a complex non-hermitian matrix.
The Eigenvalues 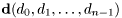 and the eigenvectors
and the eigenvectors 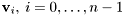 of the complex
of the complex  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
True is returned if the calculation was successful. Otherwise false.
Uses the LAPACK routine ZGEEV.
References it_error.
Calculates the eigenvalues and eigenvectors of a complex non-hermitian matrix.
The Eigenvalues 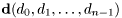 and the eigenvectors
and the eigenvectors 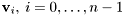 of the complex
of the complex  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
The eigenvectors are the columns of the matrix V. True is returned if the calculation was successful. Otherwise false.
Uses the LAPACK routine ZGEEV.
References it_error.
Calculates the eigenvalues of a real non-symmetric matrix.
The Eigenvalues 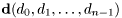 and the eigenvectors
and the eigenvectors 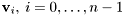 of the real
of the real  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
Uses the LAPACK routine DGEEV.
References itpp::eig().
Calculates the eigenvalues of a real non-symmetric matrix.
The Eigenvalues 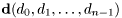 and the eigenvectors
and the eigenvectors 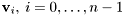 of the real
of the real  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
True is returned if the calculation was successful. Otherwise false.
Uses the LAPACK routine DGEEV.
References it_error.
Calculates the eigenvalues and eigenvectors of a real non-symmetric matrix.
The Eigenvalues 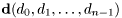 and the eigenvectors
and the eigenvectors 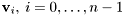 of the real
of the real  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
The eigenvectors are the columns of the matrix V. True is returned if the calculation was successful. Otherwise false.
Uses the LAPACK routine DGEEV.
References it_error.
Calculates the eigenvalues of a hermitian complex matrix.
The Eigenvalues 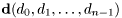 and the eigenvectors
and the eigenvectors 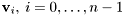 of the complex and hermitian
of the complex and hermitian  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
Uses the LAPACK routine ZHEEV.
Referenced by itpp::eig_sym().
Calculates the eigenvalues of a hermitian complex matrix.
The Eigenvalues 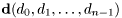 and the eigenvectors
and the eigenvectors 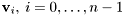 of the complex and hermitian
of the complex and hermitian  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
True is returned if the calculation was successful. Otherwise false.
Uses the LAPACK routine ZHEEV.
References it_error.
Calculates the eigenvalues and eigenvectors of a hermitian complex matrix.
The Eigenvalues 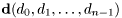 and the eigenvectors
and the eigenvectors 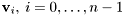 of the complex and hermitian
of the complex and hermitian  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
The eigenvectors are the columns of the matrix V. True is returned if the calculation was successful. Otherwise false.
Uses the LAPACK routine ZHEEV.
References it_error.
Calculates the eigenvalues of a symmetric real matrix.
The Eigenvalues 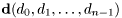 and the eigenvectors
and the eigenvectors 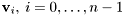 of the real and symmetric
of the real and symmetric  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
Uses the LAPACK routine DSYEV.
References itpp::eig_sym().
Calculates the eigenvalues of a symmetric real matrix.
The Eigenvalues 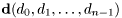 and the eigenvectors
and the eigenvectors 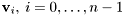 of the real and symmetric
of the real and symmetric  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
True is returned if the calculation was successful. Otherwise false.
Uses the LAPACK routine DSYEV.
References it_error.
Calculates the eigenvalues and eigenvectors of a symmetric real matrix.
The Eigenvalues 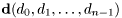 and the eigenvectors
and the eigenvectors 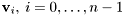 of the real and symmetric
of the real and symmetric  matrix
matrix  satisfies
satisfies
![\[ \mathbf{A} \mathbf{v}_i = d_i \mathbf{v}_i\: i=0, \ldots, n-1. \]](form_135.png)
The eigenvectors are the columns of the matrix V. True is returned if the calculation was successful. Otherwise false.
Uses the LAPACK routine DSYEV.
References it_error.
LU factorisation of real matrix.
The LU factorization of the complex matrix 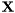 of size
of size  is given by
is given by
![\[ \mathbf{X} = \mathbf{P}^T \mathbf{L} \mathbf{U} , \]](form_143.png)
where 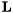 and
and 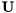 are lower and upper triangular matrices and
are lower and upper triangular matrices and 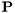 is a permutation matrix.
is a permutation matrix.
The interchange permutation vector p is such that k and p(k) should be changed for all k. Given this vector a permutation matrix can be constructed using the function
bmat permutation_matrix(const ivec &p)
If X is an n by n matrix lu(X,L,U,p) computes the LU decomposition. L is a lower triangular, U an upper triangular matrix. p is the interchange permutation vector such that elements k and row p(k) should be interchanged.
Returns true is calculation succeeds. False otherwise.
References it_error.
Referenced by itpp::det().
LU factorisation of real matrix.
The LU factorization of the real matrix 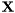 of size
of size  is given by
is given by
![\[ \mathbf{X} = \mathbf{P}^T \mathbf{L} \mathbf{U} , \]](form_143.png)
where 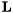 and
and 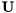 are lower and upper triangular matrices and
are lower and upper triangular matrices and 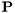 is a permutation matrix.
is a permutation matrix.
The interchange permutation vector p is such that k and p(k) should be changed for all k. Given this vector a permutation matrix can be constructed using the function
bmat permutation_matrix(const ivec &p)
If X is an n by n matrix lu(X,L,U,p) computes the LU decomposition. L is a lower triangular, U an upper triangular matrix. p is the interchange permutation vector such that k and p(k) should be changed for all k.
Returns true is calculation succeeds. False otherwise.
References it_error.
QR factorisation of a complex matrix with pivoting.
The QR factorization of the complex matrix  of size
of size 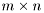 is given by
is given by
![\[ \mathbf{A} \mathbf{P} = \mathbf{Q} \mathbf{R} , \]](form_153.png)
where 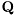 is an
is an 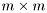 unitary matrix,
unitary matrix, 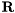 is an
is an 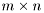 upper triangular matrix and
upper triangular matrix and 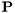 is an
is an  permutation matrix.
permutation matrix.
Returns true is calculation succeeds. False otherwise. Uses the LAPACK routines ZGEQP3 and ZUNGQR.
References it_error.
Referenced by bdm::EKFCh::bayes(), bdm::KalmanCh::bayes(), and chmat::opupdt().
QR factorisation of complex matrix with suppressed evaluation of Q.
For certain type of applications only the 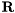 matrix of full QR factorization of the complex matrix
matrix of full QR factorization of the complex matrix 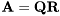 is needed. These situations arise typically in designs of square-root algorithms where it is required that
is needed. These situations arise typically in designs of square-root algorithms where it is required that 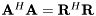 . In such cases, evaluation of
. In such cases, evaluation of 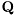 can be skipped.
can be skipped.
Modification of qr(A,Q,R).
References it_error.
QR factorisation of a complex matrix.
The QR factorization of the complex matrix  of size
of size 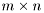 is given by
is given by
![\[ \mathbf{A} = \mathbf{Q} \mathbf{R} , \]](form_147.png)
where 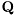 is an
is an 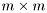 unitary matrix and
unitary matrix and 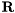 is an
is an 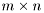 upper triangular matrix.
upper triangular matrix.
Returns true is calculation succeeds. False otherwise. Uses the LAPACK routines ZGEQRF and ZUNGQR.
References it_error.
QR factorisation of real matrix with pivoting.
The QR factorization of the real matrix  of size
of size 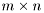 is given by
is given by
![\[ \mathbf{A} \mathbf{P} = \mathbf{Q} \mathbf{R} , \]](form_153.png)
where 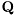 is an
is an 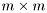 orthogonal matrix,
orthogonal matrix, 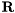 is an
is an 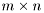 upper triangular matrix and
upper triangular matrix and 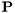 is an
is an  permutation matrix.
permutation matrix.
Returns true is calculation succeeds. False otherwise. Uses the LAPACK routines DGEQP3 and DORGQR.
References it_error.
QR factorisation of real matrix with suppressed evaluation of Q.
For certain type of applications only the 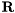 matrix of full QR factorization of the real matrix
matrix of full QR factorization of the real matrix 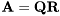 is needed. These situations arise typically in designs of square-root algorithms where it is required that
is needed. These situations arise typically in designs of square-root algorithms where it is required that 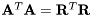 . In such cases, evaluation of
. In such cases, evaluation of 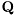 can be skipped.
can be skipped.
Modification of qr(A,Q,R).
References it_error.
QR factorisation of real matrix.
The QR factorization of the real matrix  of size
of size 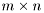 is given by
is given by
![\[ \mathbf{A} = \mathbf{Q} \mathbf{R} , \]](form_147.png)
where 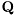 is an
is an 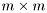 orthogonal matrix and
orthogonal matrix and 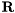 is an
is an 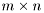 upper triangular matrix.
upper triangular matrix.
Returns true is calculation succeeds. False otherwise. Uses the LAPACK routine DGEQRF and DORGQR.
References it_error.
Schur decomposition of a complex matrix.
This function computes the Schur form of a square complex matrix 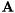 . The Schur decomposition satisfies the following equation:
. The Schur decomposition satisfies the following equation:
![\[ \mathbf{U} \mathbf{T} \mathbf{U}^{H} = \mathbf{A} \]](form_161.png)
where: 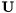 is a unitary,
is a unitary, 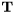 is upper triangular, and
is upper triangular, and 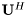 is the Hermitian transposition of the
is the Hermitian transposition of the 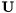 matrix.
matrix.
- Returns:
- Complex Schur matrix
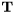
Referenced by itpp::schur().
Schur decomposition of a complex matrix.
This function computes the Schur form of a square complex matrix 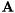 . The Schur decomposition satisfies the following equation:
. The Schur decomposition satisfies the following equation:
![\[ \mathbf{U} \mathbf{T} \mathbf{U}^{H} = \mathbf{A} \]](form_161.png)
where: 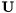 is a unitary,
is a unitary, 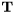 is upper triangular, and
is upper triangular, and 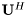 is the Hermitian transposition of the
is the Hermitian transposition of the 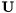 matrix.
matrix.
Uses the LAPACK routine ZGEES.
References it_error.
Schur decomposition of a real matrix.
This function computes the Schur form of a square real matrix 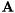 . The Schur decomposition satisfies the following equation:
. The Schur decomposition satisfies the following equation:
![\[ \mathbf{U} \mathbf{T} \mathbf{U}^{T} = \mathbf{A} \]](form_156.png)
where: 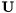 is a unitary,
is a unitary, 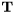 is upper quasi-triangular, and
is upper quasi-triangular, and 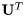 is the transposed
is the transposed 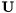 matrix.
matrix.
The upper quasi-triangular matrix may have 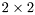 blocks on its diagonal.
blocks on its diagonal.
- Returns:
- Real Schur matrix
References itpp::schur().
Schur decomposition of a real matrix.
This function computes the Schur form of a square real matrix 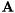 . The Schur decomposition satisfies the following equation:
. The Schur decomposition satisfies the following equation:
![\[ \mathbf{U} \mathbf{T} \mathbf{U}^{T} = \mathbf{A} \]](form_156.png)
where: 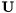 is a unitary,
is a unitary, 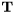 is upper quasi-triangular, and
is upper quasi-triangular, and 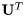 is the transposed
is the transposed 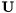 matrix.
matrix.
The upper quasi-triangular matrix may have 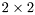 blocks on its diagonal.
blocks on its diagonal.
Uses the LAPACK routine DGEES.
References it_error.
Perform Singular Value Decomposition (SVD) of a complex matrix A.
This function returns two orthonormal matrices 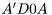 and
and 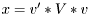 and a vector of singular values
and a vector of singular values 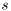 . The SVD algorithm computes the decomposition of a complex
. The SVD algorithm computes the decomposition of a complex 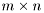 matrix
matrix  so that
so that
![\[ \mathrm{diag}(\mathbf{U}^H \mathbf{A} \mathbf{V}) = \mathbf{s} = \sigma_1, \ldots, \sigma_p \]](form_168.png)
where the elements of 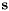 ,
, 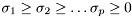 are the singular values of
are the singular values of  . Or put differently:
. Or put differently:
![\[ \mathbf{A} = \mathbf{U} \mathbf{S} \mathbf{V}^H \]](form_169.png)
where 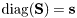
- Note:
- An external LAPACK library is required by this function.
References it_error.
Perform Singular Value Decomposition (SVD) of a real matrix A.
This function returns two orthonormal matrices 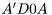 and
and 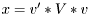 and a vector of singular values
and a vector of singular values 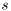 . The SVD algorithm computes the decomposition of a real
. The SVD algorithm computes the decomposition of a real 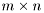 matrix
matrix  so that
so that
![\[ \mathrm{diag}(\mathbf{U}^T \mathbf{A} \mathbf{V}) = \mathbf{s} = \sigma_1, \ldots, \sigma_p \]](form_164.png)
where the elements of 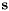 ,
, 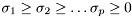 are the singular values of
are the singular values of  . Or put differently:
. Or put differently:
![\[ \mathbf{A} = \mathbf{U} \mathbf{S} \mathbf{V}^T \]](form_166.png)
where 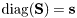
- Note:
- An external LAPACK library is required by this function.
References it_error.
Return singular values of a complex matrix A using SVD.
This function returns singular values from the SVD decomposition of a complex matrix 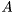 . The SVD algorithm computes the decomposition of a complex
. The SVD algorithm computes the decomposition of a complex 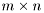 matrix
matrix  so that
so that
![\[ \mathrm{diag}(\mathbf{U}^H \mathbf{A} \mathbf{V}) = \mathbf{s} = \sigma_1, \ldots, \sigma_p \]](form_168.png)
where 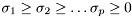 are the singular values of
are the singular values of  . Or put differently:
. Or put differently:
![\[ \mathbf{A} = \mathbf{U} \mathbf{S} \mathbf{V}^H \]](form_169.png)
where 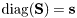
- Note:
- An external LAPACK library is required by this function.
Referenced by itpp::norm(), itpp::rank(), and itpp::svd().
Return singular values of a real matrix A using SVD.
This function returns singular values from the SVD decomposition of a real matrix 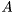 . The SVD algorithm computes the decomposition of a real
. The SVD algorithm computes the decomposition of a real 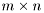 matrix
matrix  so that
so that
![\[ \mathrm{diag}(\mathbf{U}^T \mathbf{A} \mathbf{V}) = \mathbf{s} = \sigma_1, \ldots, \sigma_p \]](form_164.png)
where 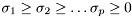 are the singular values of
are the singular values of  . Or put differently:
. Or put differently:
![\[ \mathbf{A} = \mathbf{U} \mathbf{S} \mathbf{V}^T \]](form_166.png)
where 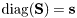
- Note:
- An external LAPACK library is required by this function.
References itpp::svd().
Get singular values s of a complex matrix A using SVD.
This function calculates singular values 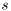 from the SVD decomposition of a complex matrix
from the SVD decomposition of a complex matrix 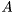 . The SVD algorithm computes the decomposition of a complex
. The SVD algorithm computes the decomposition of a complex 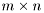 matrix
matrix  so that
so that
![\[ \mathrm{diag}(\mathbf{U}^H \mathbf{A} \mathbf{V}) = \mathbf{s} = \sigma_1, \ldots, \sigma_p \]](form_168.png)
where 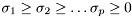 are the singular values of
are the singular values of  . Or put differently:
. Or put differently:
![\[ \mathbf{A} = \mathbf{U} \mathbf{S} \mathbf{V}^H \]](form_169.png)
where 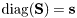
- Note:
- An external LAPACK library is required by this function.
References it_error.
Get singular values s of a real matrix A using SVD.
This function calculates singular values 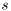 from the SVD decomposition of a real matrix
from the SVD decomposition of a real matrix 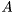 . The SVD algorithm computes the decomposition of a real
. The SVD algorithm computes the decomposition of a real 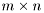 matrix
matrix  so that
so that
![\[ \mathrm{diag}(\mathbf{U}^T \mathbf{A} \mathbf{V}) = \mathbf{s} = \sigma_1, \ldots, \sigma_p \]](form_164.png)
where 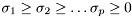 are the singular values of
are the singular values of  . Or put differently:
. Or put differently:
![\[ \mathbf{A} = \mathbf{U} \mathbf{S} \mathbf{V}^T \]](form_166.png)
where 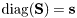
- Note:
- An external LAPACK library is required by this function.
References it_error.
 1.5.8
1.5.8