Windowing
[Signal Processing (SP) Module]
Windowing functions.
More...
Functions | |
| vec | itpp::hamming (int size) |
| Hamming window. | |
| vec | itpp::hanning (int n) |
| Hanning window. | |
| vec | itpp::hann (int n) |
| Hanning window compatible with matlab. | |
| vec | itpp::blackman (int n) |
| Blackman window. | |
| vec | itpp::triang (int n) |
| Triangular window. | |
| vec | itpp::sqrt_win (int n) |
| Square root window. | |
| vec | itpp::chebwin (int n, double at) |
| Dolph-Chebyshev window. | |
Detailed Description
Windowing functions.Function Documentation
| vec itpp::blackman | ( | int | n | ) |
Blackman window.
The n size Blackman window is a vector 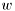 where the
where the 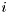 th component is
th component is
![\[ w_i = 0.42 - 0.5\cos(2\pi i/(n-1)) + 0.08\cos(4\pi i/(n-1)) \]](form_370.png)
References itpp::cos().
| vec itpp::chebwin | ( | int | n, | |
| double | at | |||
| ) |
Dolph-Chebyshev window.
The length n Dolph-Chebyshev window is a vector 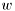 whose
whose 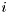 th transform component is given by
th transform component is given by
![\[ W[k] = \frac{T_M\left(\beta \cos\left(\frac{\pi k}{M}\right) \right)}{T_M(\beta)},k = 0, 1, 2, \ldots, M - 1 \]](form_373.png)
where T_n(x) is the order n Chebyshev polynomial of the first kind.
- Parameters:
-
n length of the Doplh-Chebyshev window at attenutation of side lobe (in dB)
- Returns:
- symmetric length
nDoplh-Chebyshev window
References itpp::acosh(), itpp::cheb(), itpp::cos(), itpp::cosh(), itpp::ifft_real(), itpp::is_even(), it_assert, itpp::linspace(), itpp::pow10(), itpp::reverse(), itpp::Vec< Num_T >::right(), itpp::sin(), and itpp::to_cvec().
| vec itpp::hamming | ( | int | size | ) |
Hamming window.
The n size Hamming window is a vector 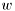 where the
where the 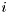 th component is
th component is
![\[ w_i = 0.54 - 0.46 \cos(2\pi i/(n-1)) \]](form_367.png)
References itpp::cos().
Referenced by itpp::fir1(), and itpp::FIR_Fading_Generator::Jakes_filter().
| vec itpp::hann | ( | int | n | ) |
Hanning window compatible with matlab.
The n size Hanning window is a vector 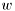 where the
where the 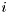 th component is
th component is
![\[ w_i = 0.5(1 - \cos(2\pi i/(n-1)) \]](form_369.png)
References itpp::cos().
| vec itpp::hanning | ( | int | n | ) |
Hanning window.
The n size Hanning window is a vector 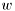 where the
where the 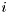 th component is
th component is
![\[ w_i = 0.5(1 - \cos(2\pi (i+1)/(n+1)) \]](form_368.png)
Observe that this function is not the same as the hann() function which is defined as in matlab.
References itpp::cos().
Referenced by itpp::spectrum().
| vec itpp::sqrt_win | ( | int | n | ) |
Square root window.
The square-root of the Triangle window. sqrt_win(n) = sqrt(triang(n))
References itpp::sqrt().
| vec itpp::triang | ( | int | n | ) |
Triangular window.
The n size triangle window is a vector 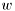 where the
where the 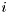 th component is
th component is
![\[ w_i = w_{n-i-1} = \frac{2(i+1)}{n+1} \]](form_371.png)
for n odd and for n even
![\[ w_i = w_{n-i-1} = \frac{2i+1}{n} \]](form_372.png)
 1.5.8
1.5.8