Theory of ARX model estimation
The ARX (AutoregRessive with eXogeneous input) model is defined as follows:
![\[ y_t = \theta' \psi_t + \rho e_t \]](form_115.png)
where 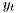 is the system output,
is the system output, ![$[\theta,\rho]$](form_116.png) is vector of unknown parameters,
is vector of unknown parameters, 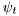 is an vector of data-dependent regressors, and noise
is an vector of data-dependent regressors, and noise 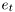 is assumed to be Normal distributed
is assumed to be Normal distributed 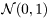 .
.
Special cases include:
- estimation of unknown mean and variance of a Gaussian density from independent samples.
Off-line estimation:
This particular model belongs to the exponential family, hence it has conjugate distribution (i.e. both prior and posterior) of the Gauss-inverse-Wishart form. See [ref]Estimation of this family can be achieved by accumulation of sufficient statistics. The sufficient statistics Gauss-inverse-Wishart density is composed of:
- Information matrix
- which is a sum of outer products
![\[ V_t = \sum_{i=0}^{n} \left[\begin{array}{c}y_{t}\\ \psi_{t}\end{array}\right] \begin{array}{c} [y_{t}',\,\psi_{t}']\\ \\\end{array} \]](form_119.png)
- "Degree of freedom"
- which is an accumulator of number of data records
![\[ \nu_t = \sum_{i=0}^{n} 1 \]](form_120.png)
On-line estimation
For online estimation with stationary parameters can be easily achieved by collecting the sufficient statistics described above recursively.
Extension to non-stationaly parameters, 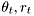 can be achieved by operation called forgetting. This is an approximation of Bayesian filtering see [Kulhavy]. The resulting algorithm is defined by manipulation of sufficient statistics:
can be achieved by operation called forgetting. This is an approximation of Bayesian filtering see [Kulhavy]. The resulting algorithm is defined by manipulation of sufficient statistics:
- Information matrix
- which is a sum of outer products
![\[ V_t = \phi V_{t-1} + \left[\begin{array}{c}y_{t}\\ \psi_{t}\end{array}\right] \begin{array}{c} [y_{t}',\,\psi_{t}']\\ \\\end{array} +(1-\phi) V_0 \]](form_122.png)
- "Degree of freedom"
- which is an accumulator of number of data records
![\[ \nu_t = \phi \nu_{t-1} + 1 + (1-\phi) \nu_0 \]](form_123.png)
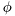 is the forgetting factor, typically
is the forgetting factor, typically ![$ \phi \in [0,1]$](form_125.png) roughly corresponding to the effective length of the exponential window by relation:
roughly corresponding to the effective length of the exponential window by relation:
![\[ \mathrm{win_length} = \frac{1}{1-\phi}\]](form_126.png)
Hence, 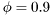 corresponds to estimation on exponential window of effective length 10 samples.
corresponds to estimation on exponential window of effective length 10 samples.
Statistics  are called alternative statistics, their role is to stabilize estimation. It is easy to show that for zero data, the statistics
are called alternative statistics, their role is to stabilize estimation. It is easy to show that for zero data, the statistics 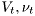 converge to the alternative statistics.
converge to the alternative statistics.
Structure estimation
For this model, structure estimation is a form of model selection procedure. Specifically, we compare hypotheses that the data were generated by the full model with hypotheses that some regressors in vector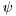 are redundant. The number of possible hypotheses is then the number of all possible combinations of all regressors.
are redundant. The number of possible hypotheses is then the number of all possible combinations of all regressors.
However, due to property known as nesting in exponential family, these hypotheses can be tested using only the posterior statistics. (This property does no hold for forgetting 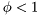 ). Hence, for low dimensional problems, this can be done by a tree search (method bdm::ARX::structure_est()). Or more sophisticated algorithm [ref Ludvik]
). Hence, for low dimensional problems, this can be done by a tree search (method bdm::ARX::structure_est()). Or more sophisticated algorithm [ref Ludvik]
Software Image
Estimation of the ARX model is implemented in class bdm::ARX.- models from exponential family share some properties, these are encoded in class bdm::BMEF which is the parent of ARX
- one of the parameters of bdm::BMEF is the forgetting factor which is stored in attribute
frg, - posterior density is stored inside the estimator in the form of bdm::egiw
- references to statistics of the internal
egiwclass, i.e. attributesVandnuare established for convenience.
How to try
The best way to experiment with this object is to run matlab scriptarx_test.m located in directory estimator with ARX data fields for detailed description.
- In default setup, the parameters converge to the true values as expected.
- Try changing the forgetting factor, field
estimator.frg, to values <1. You should see increased lower and upper bounds on the estimates. - Try different set of parameters, filed
system.theta, you should note that poles close to zero are harder to identify.
 1.5.8
1.5.8