Examples of (extended) Kalman filtering

Kalman filtering and Extended Kalman filtering are special cases of Bayesian filtering. The Kalman filter is optimal for linear state space model with Gaussian disturbances, the extended Kalman filter is derived as linearization of non-linear state space models with Gaussian noises. Hence it is only sub-optimal filter.

More advanced filtering algorithms for non-linear non-Gaussian models can be derived, see ...

Kalman Filtering

Kalman filtering is optimal estimation procedure for linear state space model:

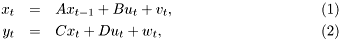
$\begin{eqnarray} x_t &= &A x_{t-1} + B u_{t} + v_t,\\ y_t &= &C x_{t} + D u_{t} + w_t, \end{eqnarray}$

where 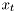$ x_t $ is the state, 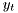$ y_t $ is the system output, 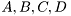$ A, B, C, D$ are state matrices of appropriate dimensions, 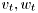$v_t, w_t$ are zero mean Gaussian noises with covariance matrices 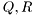$Q, R$ , respectively.

Both prior and posterior densities on the state are Gaussian, i.e. of the class enorm.

There is a range of classes that implements this functionality, namely:

bdm::KalmanFull which implements the estimation algorithm on full matrices,
bdm::KalmanCh which implements the estimation algorithm using choleski decompositions and QR algorithm.

Extended Kalman Filtering

Extended Kalman filtering arise by linearization of non-linear state space model:

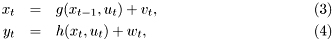
$\begin{eqnarray} x_t &= &g( x_{t-1}, u_{t}) + v_t,\\ y_t &= &h( x_{t} , u_{t}) + w_t, \end{eqnarray}$

where 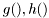$ g(), h() $ are general non-linear functions which have finite derivatives. Remaining variables have the same meaning as in the Kalman Filter.

In order to use this class, the non-linear functions and their derivatives must be defined as an instance of class diffbifn.

Two classes are defined:

bdm::EKFfull on full size matrices,
bdm::EKFCh on Choleski decompositions and using QR algorithm.

Examples of Use

The classes can be used directly in C++ or via User Info. The latter example is illustrated in file estimator. A very short example of the former follows:

#include "estim/kalman.h"
using namespace bdm;
        
// estimation of AR(0) model
int main() {
        //dimensions
        int dx=3, dy=3, du=1;
        // matrices
        mat A = eye(dx);
        mat B = zeros(dx,du);
        mat C = eye(dx);
        mat D = zeros(dy,du);
        mat Q = eye(dx);
        mat R = 0.1*eye(dy);
        //prior
        mat P0 = 100*eye(dx);
        vec mu0 = zeros(dx);
        // Estimator
        KalmanCh KF;
        KF.set_parameters(A,B,C,D,/*covariances*/ Q,R);
        KF.set_statistics(mu0,P0);
        // Estimation loop
        for (int i=0;i<100;i++){
                KF.bayes(randn(dx+du));
        }
        //print results
        cout << "Posterior estimate of x is: "  << endl;
        cout << "mean: "<< KF.posterior().mean()<< endl;
        cout << "variance: "<< KF.posterior().variance()<< endl;
}