bdm::egiw Class Reference
Gauss-inverse-Wishart density stored in LD form. More...
Detailed Description
Gauss-inverse-Wishart density stored in LD form.
For 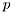 -variate densities, given rv.count() should be
-variate densities, given rv.count() should be 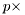 V.rows().
V.rows().
#include <exp_family.h>
Public Member Functions | |
| vec | sample () const |
Returns a sample, 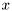 from density from density 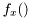 . . | |
| vec | mean () const |
| return expected value | |
| vec | variance () const |
| return expected variance (not covariance!) | |
| vec | est_theta () const |
LS estimate of 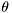 . . | |
| ldmat | est_theta_cov () const |
| Covariance of the LS estimate. | |
| void | mean_mat (mat &M, mat &R) const |
expected values of the linear coefficient and the covariance matrix are written to M and R , respectively | |
| double | evallog_nn (const vec &val) const |
| In this instance, val= [theta, r]. For multivariate instances, it is stored columnwise val = [theta_1 theta_2 ... r_1 r_2 ]. | |
| double | lognc () const |
logarithm of the normalizing constant, 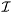 | |
| void | pow (double p) |
| Power of the density, used e.g. to flatten the density. | |
| virtual double | evallog (const vec &val) const |
| Evaluate normalized log-probability. | |
| virtual vec | evallog_m (const mat &Val) const |
| Evaluate normalized log-probability for many samples. | |
| virtual vec | evallog_m (const Array< vec > &Val) const |
| Evaluate normalized log-probability for many samples. | |
| virtual string | to_string () |
| This method returns a basic info about the current instance. | |
| virtual void | to_setting (Setting &set) const |
| This method save all the instance properties into the Setting structure. | |
| virtual void | validate () |
| This method TODO. | |
Constructors | |
| egiw () | |
| egiw (int dimx0, ldmat V0, double nu0=-1.0) | |
| void | set_parameters (int dimx0, ldmat V0, double nu0=-1.0) |
Access attributes | |
| ldmat & | _V () |
| const ldmat & | _V () const |
| double & | _nu () |
| const double & | _nu () const |
| void | from_setting (const Setting &set) |
| Load from structure with elements:. | |
Constructors | |
Construction of each epdf should support two types of constructors:
The following constructors should be supported for convenience:
All internal data structures are constructed as empty. Their values (including sizes) will be set by method | |
| void | set_parameters (int dim0) |
Matematical Operations | |
| virtual mat | sample_m (int N) const |
Returns N samples, 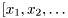 from density from density 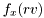 . . | |
| virtual shared_ptr< mpdf > | condition (const RV &rv) const |
| Return conditional density on the given RV, the remaining rvs will be in conditioning. | |
| virtual shared_ptr< epdf > | marginal (const RV &rv) const |
| Return marginal density on the given RV, the remainig rvs are intergrated out. | |
| virtual void | qbounds (vec &lb, vec &ub, double percentage=0.95) const |
Lower and upper bounds of percentage % quantile, returns mean-2*sigma as default. | |
Connection to other classes | |
| void | set_rv (const RV &rv0) |
| Name its rv. | |
| bool | isnamed () const |
| True if rv is assigned. | |
| const RV & | _rv () const |
| Return name (fails when isnamed is false). | |
Access to attributes | |
| int | dimension () const |
| Size of the random variable. | |
Protected Attributes | |
| ldmat | V |
| Extended information matrix of sufficient statistics. | |
| double | nu |
| Number of data records (degrees of freedom) of sufficient statistics. | |
| int | dimx |
| Dimension of the output. | |
| int | nPsi |
| Dimension of the regressor. | |
| int | dim |
| dimension of the random variable | |
| RV | rv |
| Description of the random variable. | |
Member Function Documentation
| void bdm::egiw::from_setting | ( | const Setting & | set | ) | [inline, virtual] |
Load from structure with elements:.
{ rv = {class="RV", names=(...),}; // RV describing meaning of random variable
// elements of offsprings
}
Reimplemented from bdm::epdf.
References dimx, bdm::UI::get(), nu, bdm::epdf::rv, and bdm::epdf::set_rv().
The documentation for this class was generated from the following files:
- exp_family.h
- exp_family.cpp
 1.6.1
1.6.1