bdm::elognorm Class Reference
#include <exp_family.h>
Public Member Functions | |
| vec | sample () const |
Returns a sample, 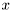 from density from density 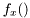 . . | |
| vec | mean () const |
| return expected value | |
| virtual double | evallog (const vec &val) const |
| Evaluate normalized log-probability. | |
| virtual vec | evallog_m (const mat &Val) const |
| Evaluate normalized log-probability for many samples. | |
| virtual vec | evallog_m (const Array< vec > &Val) const |
| Evaluate normalized log-probability for many samples. | |
| virtual void | pow (double p) |
| Power of the density, used e.g. to flatten the density. | |
| virtual string | to_string () |
| This method returns a basic info about the current instance. | |
| virtual void | to_setting (Setting &set) const |
| This method save all the instance properties into the Setting structure. | |
Constructors | |
| void | set_parameters (const vec &mu, const ldmat &R) |
| void | from_setting (const Setting &root) |
| void | validate () |
| This method TODO. | |
Constructors | |
Construction of each epdf should support two types of constructors:
set_parameters(). This way references can be initialized in constructors. | |
| void | set_parameters (int dim0) |
Mathematical operations | |
| void | dupdate (mat &v, double nu=1.0) |
| dupdate in exponential form (not really handy) | |
| double | evallog_nn (const vec &val) const |
| Evaluate normalized log-probability. | |
| double | lognc () const |
logarithm of the normalizing constant, 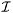 | |
| vec | variance () const |
| return expected variance (not covariance!) | |
| shared_ptr< mpdf > | condition (const RV &rvn) const |
| Return conditional density on the given RV, the remaining rvs will be in conditioning. | |
| void | condition (const RV &rvn, mpdf &target) const |
| shared_ptr< epdf > | marginal (const RV &rvn) const |
| Return marginal density on the given RV, the remainig rvs are intergrated out. | |
| void | marginal (const RV &rvn, enorm< ldmat > &target) const |
Access to attributes | |
| vec & | _mu () |
| const vec & | _mu () const |
| void | set_mu (const vec mu0) |
| ldmat & | _R () |
| const ldmat & | _R () const |
Matematical Operations | |
| virtual mat | sample_m (int N) const |
Returns N samples, 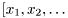 from density from density 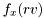 . . | |
| virtual void | qbounds (vec &lb, vec &ub, double percentage=0.95) const |
Lower and upper bounds of percentage % quantile, returns mean-2*sigma as default. | |
Connection to other classes | |
Description of the random quantity via attribute rv is optional. For operations such as sampling rv does not need to be set. However, for marginalization and conditioning rv has to be set. NB: | |
| void | set_rv (const RV &rv0) |
| Name its rv. | |
| bool | isnamed () const |
| True if rv is assigned. | |
| const RV & | _rv () const |
| Return name (fails when isnamed is false). | |
Access to attributes | |
| int | dimension () const |
| Size of the random variable. | |
Protected Attributes | |
| vec | mu |
| mean value | |
| ldmat | R |
| Covariance matrix in decomposed form. | |
| int | dim |
| dimension of the random variable | |
| RV | rv |
| Description of the random variable. | |
Detailed Description
Log-Normal probability density only allow diagonal covariances!
Density of the form 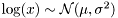 , i.e.
, i.e.
![\[ x \sim \frac{1}{x\sigma\sqrt{2\pi}}\exp{-\frac{1}{2\sigma^2}(\log(x)-\mu)} \]](form_96.png)
Function from_setting loads mu and R in the same way as it does for enorm<>!
Member Function Documentation
| void bdm::enorm< ldmat >::from_setting | ( | const Setting & | root | ) | [virtual, inherited] |
Create Normal density
![\[ f(rv) = N(\mu, R) \]](form_164.png)
from structure
class = 'enorm<ldmat>', (OR) 'enorm<chmat>', (OR) 'enorm<fsqmat>'; mu = []; // mean value R = []; // variance, square matrix of appropriate dimension
Reimplemented from bdm::epdf.
The documentation for this class was generated from the following file:
 1.5.9
1.5.9