mgamma_fix Class Reference

Gamma random walk around a fixed point. More...

#include <libEF.h>

Inheritance diagram for mgamma_fix:

Inheritance graph
[legend]
Collaboration diagram for mgamma_fix:

Collaboration graph
[legend]

List of all members.

Public Member Functions

 mgamma_fix (const RV &rv, const RV &rvc)
 Constructor.
void set_parameters (double k0, vec ref0, double l0)
 Set value of k.
void condition (const vec &val)
 Update ep so that it represents this mpdf conditioned on rvc = cond.
void set_parameters (double k)
 Set value of k.
vec samplecond (vec &cond, double &lik)
 Generate one sample of the posterior.
mat samplecond (vec &cond, vec &lik, int n)
 Generate matrix of samples of the posterior.
virtual double evalcond (const vec &dt, const vec &cond)
 Shortcut for conditioning and evaluation of the internal epdf. In some cases, this operation can be implemented efficiently.
RV _rvc ()
 access function
epdf & _epdf ()
 access function

Protected Attributes

double l
vec refl
egamma epdf
 Internal epdf that arise by conditioning on rvc.
double k
 Constant $k$.
vec * _beta
 cache of epdf.beta
RV rv
 modeled random variable
RV rvc
 random variable in condition
epdf * ep
 pointer to internal epdf

Detailed Description

Gamma random walk around a fixed point.

Mean value, 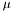$\mu$, of this density is given by a geometric combination of rvc and given fixed point, $p$. $k$ is the coefficient of the geometric combimation

\[ \mu = \mu_{t-1} ^{l} p^{1-l}\]

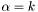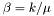Standard deviation of the random walk is proportional to one $k$-th the mean. This is achieved by setting $\alpha=k$ and $\beta=k/\mu$.

The standard deviation of the walk is then: 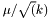$\mu/\sqrt(k)$.

The documentation for this class was generated from the following file:
Generated on Fri Apr 18 11:15:21 2008 for mixpp by  doxygen 1.5.3